Sum to Infinity Geometric Progression

By Bio_Alia464 01 Sep, 2022 Post a Comment

Most mathematical activity involves the use of pure. How do we check whether a series is an arithmetic progression or not.

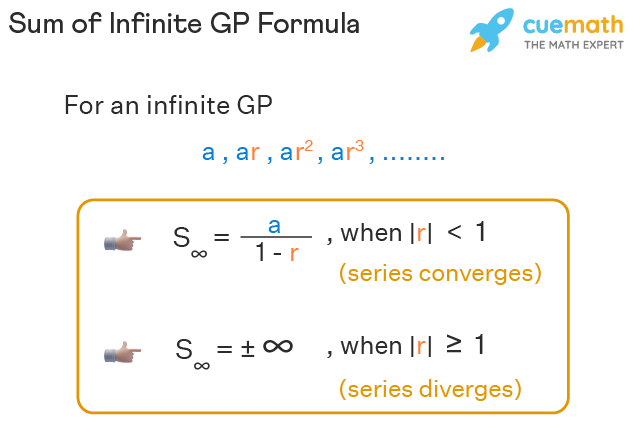
Sum Of Infinite Gp Formula Sum Of Infinite Terms Of Gp

The Product of all the numbers present in the geometric progression gives us the overall product.

. The infinite sequence of additions implied by a series cannot be effectively carried on at least in a finite amount of time. Consider an AP consisting n terms. S n n22a n 1 d This is.

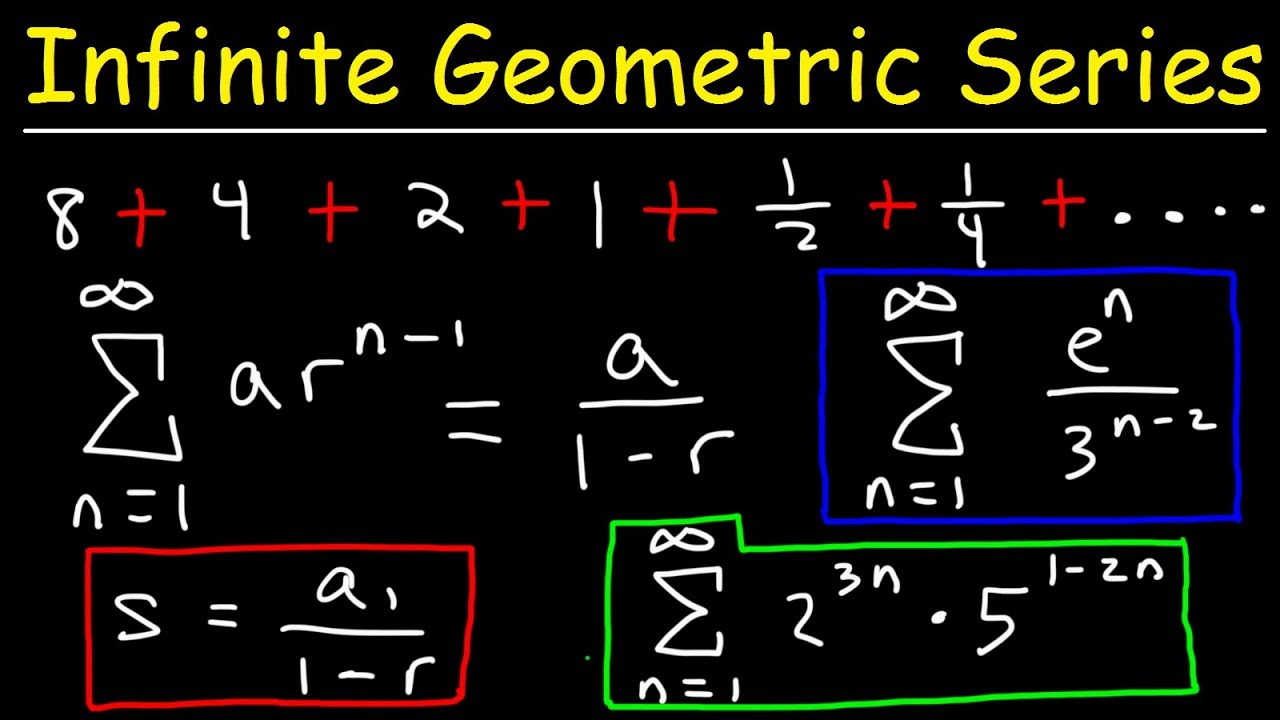
Sum to n Terms of a GP. It is very useful while calculating the Geometric mean of the entire. Letting a be the first term here 2 n be the number of terms here 4 and r be the constant that each term is multiplied by to get the next term here 5 the sum is given by.

An arithmetic-geometric progression AGP is a progression in which each term can be represented as the product of the terms of an arithmetic progressions AP and a geometric progressions GP. In mathematics a series is the sum of the terms of an infinite sequence of numbers. Thus the explicit formula is.

If r 1 r 1 r 1 then the sum to infinity is given by. In mathematics a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. The formula for the nth term of a geometric progression whose first term is a and common ratio is r is a n ar n1.

In the example above this gives. Arithmetic Progression Sum of Nth terms of GP. Sum of elements of a Geometric Progression GP in a given range.

Instinctively this sum of infinite numbers will be equal to infinity. Sum to infinity of the series 3 2 6 5 3 2 2 4 1 1. 64 16 4 1.

That means that when. 4 4 4 4 B. For example the series is geometric because each successive term can be obtained by multiplying the previous term by In general a geometric series is written as where is the coefficient of each term and is the common ratio.

When you want to take the sum of all terms of the sequence then it will be the sum of infinite numbers. The sum of the infinite GP formula is given as S n a1r where r. For Infinite Geometric Series.

We can use this formula. The infinite sum of an infinite geometric series formula is often infinity either positive or negative infinity. View solution The sum of the infinite series 1 2.

Now learn how t o add GP if there are n number of terms present in it. It is known that the sum of the first n elements of geometric progression can be calculated by the formula. In geometry the tangent line or simply tangent to a plane curve at a given point is the straight line that just touches the curve at that point.

Product of the Geometric series. Sum of N-terms of geometric progression for larger values of N Set 2 Using recursion 27 Apr 20. The formula for the n th term of an AP.

More precisely a straight line is said to be a tangent of a curve y fx at a point x c if the line passes through the point c fc on the curve and. A Sequence is a set of things usually numbers that are in order. .

The sum to infinity of a geometric progression. While looking for a sum of an arithmetic sequence it becomes essential to pick the value of n to calculate the partial sum. 11X1 T10 03 arithmetic geometric means.

Arithmetic Series to Infinity. Sum of the first n terms S n. Geometric Progression GP.

Where b 1 - is the first element of the geometric series in our case it. The family of natural numbers includes all the counting numbers starting from 1 till infinity. Lesson 4 - Geometric Shapes.

Knowledge study learning is an area of knowledge that includes such topics as numbers arithmetic and number theory formulas and related structures shapes and the spaces in which they are contained and quantities and their changes calculus and analysis. Here a is the first term and r is the common ratio. Copy and paste this code into your website.

If a is the initial term and d is a common difference. Find the sum to infinity of each geometric sequence if it exists. Where r is a constant which is known as common ratio and none of the terms in the sequence is zero.

Furthermore when many random variables are sampled and the most extreme results are intentionally. A geometric series is the sum of the numbers in a geometric progression. Nth Term of a GP.

A geometric series is a sum of an infinite number of terms such that the ratio between successive terms is constant. Sum Of N Terms. Greater than 1 there will be exponential growth towards positive or negative infinity depending on the sign of the initial term.

So what happens when n goes to infinity. The formula works for any real numbers a and r except r 1. But be careful.

Lesson 14 - What is Infinity in Math. There are various formulae and techniques for the calculation of the sum of squares. Therefore to calculate series sum one needs somehow to find the expression of the partial series sum S nIn our case the series is the decreasing geometric progression with ratio 13.

Only when a certain condition is. Grade 10 Science Module 1st Quarter Luwen Borigas. Geometric Sequences and Sums Sequence.

A series is convergent or converges if the sequence of its partial sums tends to a limit. That is. Problems based on Sum to n.

N will tend to Infinity n Putting this in the generalized formula. Leibniz defined it as the line through a pair of infinitely close points on the curve. Geometric Progression Sum Of Gp.

Each successive term is obtained in a geometric progression by multiplying the common ratio to its preceding term. In other words if you keep adding together the terms of the sequence forever you will get a finite value. In statistics regression toward the mean also called reversion to the mean and reversion to mediocrity is a concept that refers to the fact that if one sample of a random variable is extreme the next sampling of the same random variable is likely to be closer to its mean.

Then the member terms grow towards negative infinity. The list of formulas related to GP is given below which will help in solving different types of problems. 8 terms of 3 3 3 3.

More precisely an infinite sequence defines a series S that is denoted. The n th partial sum S n is the sum of the first n terms of the sequence. In arithmetic we often come across the sum of n natural numbers.

The sum of the first n terms of the AP series. A n ar n-1. Lesson 31 - Triangle Sum Theorem Proof Triangle Sum Theorem Proof.

1 the progression is a constant sequence. In geometric progressions where r 1 in other words where r is less than 1 and greater than 1 the sum of the sequence as n tends to infinity approaches a value. The formula for the sum of n terms of AP.

Mathematics from Ancient Greek μάθημα. However if the set to which the terms and their finite sums belong has a notion of limit it is sometimes possible to assign a value to a series called the sum of the seriesThis value is the limit as n tends to infinity if the limit exists of the finite sums of. The general form of terms of a GP is a ar ar 2 ar 3 and so on.

This is called the geometric progression formula of sum to infinity. If n consecutive natural numbers. And r should not be 0 because the sequence a00 is not geometric.

So our infnite geometric series has a finite sum when the ratio is less than 1. N th term for the GP. The arithmetic and geometric progression Maija Liepa.

The formula for the arithmetic progression sum is explained below. Geometric series Jhon Paul Lagumbay. S n b 1 q n 1 q 1.

Prove The Infinite Geometric Series Formula Sum Ar N A 1 R Youtube